Triângulos: congruência e pontos notáveis
Congruência de figuras planas
Já trabalhamos com:
• Segmentos congruentes: têm mesma medida.
• Ângulos congruentes: têm mesma medida.
O que seriam figuras planas congruentes?
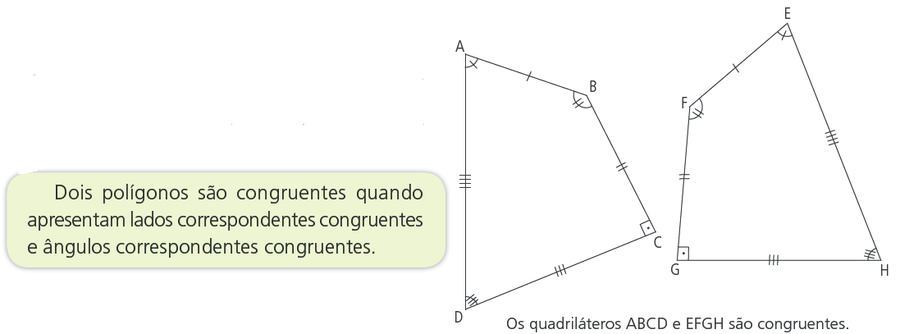
Se você copiar e recortar os quadriláteros ao lado, verá que eles se sobrepõem perfeitamente, ou seja, coincidem.
Duas figuras planas são congruentes se quando sobrepostas coincidem ponto a ponto.
Neste tópico trataremos da congruência de polígonos, em especial de triângulos. Com auxílio de régua e transferidor, meça os lados e os ângulos internos dos quadriláteros ABCD e EFGH. Anote os valores em seu caderno, em uma tabela.


A cada ângulo do quadrilátero ABCD corresponde um ângulo do quadrilátero EFGH, que é congruente a ele.
A cada lado do quadrilátero ABCD corresponde um lado do quadrilátero EFGH, que é congruente a ele.
Por exemplo, ao ângulo A corresponde o ângulo E e vice-versa. Usaremos “tracinhos” para identificar pares de lados e pares de ângulos correspondentes. Veja na figura ao lado.
Casos de congruência de triângulos
Triângulos são polígonos, portanto, para que dois triângulos sejam congruentes precisamos ter lados correspondentes congruentes e ângulos correspondentes congruentes.
Para decidirmos se dois triângulos são ou não congruentes, precisamos verificar 6 condições:
• 3 congruências entre lados correspondentes;
• 3 congruências entre ângulos correspondentes.
No entanto, os triângulos apresentam características que permitirão reduzir esse trabalho.
Caso LLL

Caso ALA

Caso LAL














0 Comentários